5.1 렌더링 파이프 라인의 개요

Directx12 3D 프로그래밍 입문/5. 렌더링 파이프 라인

5.1 렌더링 파이프 라인의 개요

ftftgop3 2023. 11. 13. 00:03

렌더링 파이프 라인 단계 ← 자원 메모리 풀 (GPU 자원을 입력)

렌더링 파이프 라인 단계 → 자원 메모리 풀 ( GPU 자원을 기록)

양방향 일때는 자원을 입력 및 기록을 동시에 일어 난다

GPU 의 자원도 사용

입력 조립기, Input assembler, IA정점 버퍼 : 정점 데이터를 순차적으로 저장 하는 공간

//명령 목록 기본 도형 위상 구조 설정, 
//현재 삼각형 
mCommandList->IASetPrimitiveTopology(D3D11_PRIMITIVE_TOPOLOGY_TRIANGLELIST);
//선 목록
mCommandList->IASetPrimitiveTopology(D3D11_PRIMITIVE_TOPOLOGY_LINELIST);
//삼각형 띠
mCommandList->IASetPrimitiveTopology(D3D11_PRIMITIVE_TOPOLOGY_TRIANGLESTRIP);

점 목록, 선 띠, 선 목록, 삼각형 띠 ,삼각형 목록

홀수 번째는 시계 반향으로 정점들을 이어준다.
짝수 번째는 반 시계 반향으로 정점들을 이어준다.
인접 삼각형 : 주어진 삼각형으로 인접한 삼각형 목록
기하 셰이더 알고리즘 구현 때 주어진 삼각형에서 인접 삼각형을 추가

색인

여러 정점들의 감기는 순서를 저장

정점 버퍼의 데이터와 비슷한 역할을 하지만 정점 구조체를 계속 추가하는 것 보다

적은 메모리를 사용, 정점 들이 적절한 순서로 캐시에 저장 되면

그래픽 하드웨어는 중복된 정점 들을 처리 할 필요가 없다

사용 이유 : 메모리 요구량 저하, 그리팩 하드웨어 처리량 감소

삼각형 띠에서는 삼각형 그리는 순서(감기는 순서)가 달라진다.

기본도형 위상 구조 설정 (삼각형 목록 주로 사용)

메모리에서 정점 및 인덱스를 읽어서 기본 도형 조립

정점 셰이더

정점 하나를 받아서 정점을 출력 하는 함수 생각해도 된다.
프로그래머가 작성 후 GPU 제출 하고
함수는 정점에 대해 GPU에서 실행 하기 때문에 빠르다.
텍스처, 광원 정점 자료 등 GPU 메모리에 담긴 다른 자료들을 접근 가능

국소 공간 과 세계 공간

국소 공간 : 좌표계의 원점이 물체의 중심을 나타낸다 (local space)

국소 공간 장점

물체의 중심이 원점과 일치

인스터싱 : 한 물체의 기하 구조를 가지고 물체 개별의 인스턴스 마다 이동 크기 회전을 다르게 세계 공간에 렌더링 하는 효율 적인 기법

세계 공간

국소 좌표계 있는 인스턴스들을 하나의 좌표계로 정렬

W = SRT 하나의 행렬로 표현 할 수 있다

시야 공간

시야 공간 의미 세계 공간을 카메라로 보이는 영역을 결정

시야 공간 : 가상 카메라에 국소 좌표계 를 부여 하면 그게 시야 좌표계, 시야 공간

시야 변환 : 세계 공간에서 시야 공간으로 변환

렌더링 파이프라인 후반부 단계에서 시야 공간 기준으로 서술하는 것이 편한 경우가 많다.

시야 좌표계 에서 세계 좌표계로 변환 W 라고 하면 반대로 시야 좌표계에서 세계 좌표계는 W의 역행렬

W = SRT 이며 일반적으로 세계 좌표계에서 시야 좌표계는 위치와 방향만 차이

W = RT (회전 후 이동 순서)

$$ W=RT\\=\begin{bmatrix}u_x & u_y & u_z & 0 \\v_x & v_y & v_z & 0\\w_x & w_y & w_z & 0\\Q_x & Q_y & Q_z & 1 \\\end{bmatrix} $$

회전 행렬의 역행렬은 직교 행렬이기 때문에 전치 행렬로 변환 후 연산

$$ V=W^{-1} = (RT)^{-1}=T^{-1}R^{-1}=T^{-1}R^T\\=\begin{bmatrix}1 & 0 & 0 & 0 \\0 & 1 & 0 & 0 \\0 & 0 & 1 & 0 \\-Q_x & -Q_y & -Q_z & 1 \\\end{bmatrix}\begin{bmatrix}u_x & v_x & w_x & 0 \\u_y & v_y & w_y & 0 \\u_z & v_z & w_z & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}\\=\begin{bmatrix}u_x & v_x & w_x & 0 \\u_y & v_y & w_y & 0 \\u_z & v_z & w_z & 0 \\-Q\bullet u & -Q\bullet v & -Q\bullet w & 1 \\\end{bmatrix} $$

T : 카메라가 바라보는 지점,

Q : 카메라 위치(원점),

j : 세계 공간의 위쪽(0 , 1, 0) 연산

$$ w=\frac{T-Q}{\left\|T-Q \right\|} \ U =\frac{j-w}{\left\|j-w \right\|} \ v=w\ast u $$

//시야 행렬 V 출력
inline XMMATRIX XM_CALLCONV XMMatrixLookAtLH
(
    FXMVECTOR EyePosition, //입력 카메라 Q
    FXMVECTOR FocusPosition, // 대상 점 T
    FXMVECTOR UpDirection//세계 상향 벡터 j
)
XMVECTOR pos = XMVectorSet(x, y, z, 1.0f); //원점
XMVECTOR target = XMVectorZero();//대상 점
XMVECTOR up = XMVectorSet(0.0f, 1.0f, 0.0f, 0.0f); //세계 상향 벡터

XMMATRIX view = XMMatrixLookAtLH(pos, target, up);

투영과 동차 절단 공간

투영 : 카메라의 절두체 안에 3차원 기하 구조를 2차원 투영창에 투영

편형선들이 하나의 소실점에 수렴, 깊이에 따라 투영의 크기 변화

원근 투영 변환 : 3차원 정점 v에서 연결된 투영선이 2차원 투영 평면에 만나는 점 V’ 로 변환

절두체 정의

원점 기준으로 양의 Z 축을 바라보는 절두체를 4가지 수량으로 정의

Near Plane : 원점과 가까운 평면 사이의 거리

Far Plane : 먼 평면 사이의 거리

수직 시야각 a, 종횡비 r

종횡비 r = w/h 정의 투영창의 너비와 높이를 뜻하고 후면 버퍼에 사상 되기 때문에 후면 버퍼와 종횡비는 일치

투영창의 너비는 : 2r, 높이는 2로 가정

수평 시야각 B를 구하는 공식

$$ r=\frac{w}{h}= \frac{w}{2} => w=2r\\tan(\frac{a}{2})=\frac{1}{d} =>d=cot(\frac{a}{2})\\tan(\frac{B}{2})=\frac{r}{d}=\frac{r}{cot(\frac{a}{2})}=rtan((\frac{a}{2}))\\B=2tan^{-1}(rtan\frac{a}{2})) $$

정점의 투영 공식

닮은꼴 삼각형 원리를 적용 후 연산

$$ \frac{x'}{d} = \frac{x}{z}=>x'=\frac{xd}{z}=\frac{xcot(a/2)}{z}=\frac{x}{ztan(a/2)}\\\frac{y'}{d} = \frac{y}{z}=>x'=\frac{yd}{z}=\frac{ycot(a/2)}{z}=\frac{y}{ztan(a/2)}\\ $$

이때 점의 (x,y,z) 절두체 안에 있는 필요 충분 조건

$-r<=x'<=r \\-1 <=y'<=1\\n<=z'<=f$

정규화된 장치 좌표 (NDC)

위의 계산은 문제점은 투영 창의 크기가 종횡비 에 의존

하드웨어가 종횡비를 소프트웨어에 알려줘야 하는데 그 의존성을 사라지게 하는 한다.

NCD 의 특징은 투영창의 높이, 너비 2로 고정

하드웨어에 투영 좌표를 공급 할때 NDC 로 정규환된 좌표를 보내야 한다.

정규화된 장치 좌표 (x 값에 r: 종횡비를 나눈 값)

$-r<=x'/r<=r \\-1 <=y'<=1\\n<=z'<=f$

투영 공식에 NDC 좌표 성분을 직접 얻을 수 있다.

$$ x' = \frac{x}{rztan(a/2)}\\y' = \frac{y}{ztan(a/2)}\\ $$

투영 변환을 행렬 표현

NDC 공식을 바로 행렬로 표현 할 수 없다 ( 비 선형 공식)

2단계로 나누어서 선형 과 비선형으로 나눈 후 행렬로 표현

비선형 공식 : 식을 Z로 나누기

투영 시 z 값도 정규화 하기 떄문에 값이 남지 않는다.

비 선형 공식에는 Z 값이 필요 하기때문에 성분 [2][3]에 1의 값이 들어 간다.

전체 투영 변환의 선형 부분$$ [x,y,z,1]\begin{bmatrix}\frac{1}{rtan(a/2)} & 0 & 0 & 0 \\0 & \frac{1}{tan(a/2)} & 0 & 0 \\0 & 0 & A & 1 \\0 & 0 & B & 0 \\\end{bmatrix}\\=[\frac{1}{rtan(a/2)},\frac{1}{tan(a/2)}, Az+B,z] $$
A ,B : 정규화 된 깊이 값에서 사용
투영 변환의 비 선형 부분
w 를 나눈 형태를 원근 나누기 및 동차 나누기 라고 한다

$$[\frac{1}{rtan(a/2)},\frac{1}{tan(a/2)}, Az+B,z]\to [\frac{1}{rztan(a/2)},\frac{1}{ztan(a/2)}, A+\frac{B}{z},1] $$

정규화된 깊이 값

투영된 x,y 성분을 일정 구간으로 정규화 과정 [-1, 1]

z 값은 [n, f]을 [0, 1]로 정규화 변환 시켜야 한다

$g(z) = A+\frac{B}{z}$

조건 1: $g(n) = A + B/n = 0$ (가까운 평면이 0으로 사상)

조건 2:$g(f) = A+B/f =1$ (먼 평면 1로 사상)

$$ B = -An\\A + \frac{-An}{f} = 1\\\frac{Af-An}{f} =1\\Af-An =f\\A = \frac{f}{f-c}\\g(z) = \frac{f}{f-c} - \frac{nf}{(f-n)z} $$

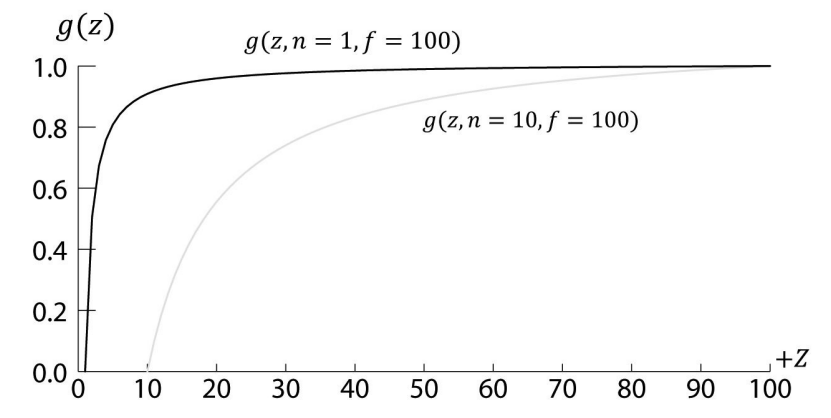
함수는 순증가 함수이자 비선형 함수임을 보여준다

아래의 함수를 보몀ㄴ 깊이 값 대부분 작은 부분 집합에 몰려 있다

일반적으로 가까운 평면과 먼 평면을 최대한 가깝게 해서 깊이 정밀 문제를 최소화

함수 그래프

최종 투영 행렬

이 투영 행렬의 곱한 후가 동차 절단 공간 및 투영 공간에 있다고 한다

그 후 동차 나누기 를 하면 정규환된 장치 좌표 (NDC) 공간에 있다고 한다.

$$ P = \begin{bmatrix}\frac{1}{rtan(a/2)} & 0 & 0 & 0 \\0 & \frac{1}{tan(a/2)} & 0 & 0 \\0 & 0 & \frac{f}{f-n} & 1 \\0 & 0 & \frac{-nf}{f-n} & 0 \\\end{bmatrix} $$

inline XMMATRIX XM_CALLCONV XMMatrixPerspectiveFovLH
(
    float FovAngleY, //수직 시야각(라디안 단위)
    float AspectRatio,//종횡비 
    float NearZ,//가까운 평면 거리
    float FarZ//먼 평면 거리
)
//수직 시야각 45도, 종횡비 함수, 가까운 평면 1, 먼 평면 1000
XMMATRIX P = XMMatrixPerspectiveFovLH(0.25f * XM_PI, AspectRatio(), 1.0f, 1000.0f)

float D3DApp::AspectRatio()const
{
	return static_cast<float>(mClientWidth) / mClientHeight;
}

참고 및 내용 인용
프랭크 D 루나 지음, 류광 옮김
한빛 미디어
Directx 12를 이용한 3D 게임 프로그래밍 입문(2017)